بسیاری از فرآیندهای طبیعی از جمله ترکیب ساختار بدن موجودات زنده نظم مشخصی دارند و از دنبالهی اعدادی تبعیت میکنند که امروزه با نام دنبالهی اعداد فیبوناچی (فیبوناتچی - Fibonacci) شناخته میشود. مشهورترین خاصیت این اعداد نسبت دو جملهی متوالی آنها به ازای جملات بزرگ دنباله است که به عدد طلایی مشهور است.
این دنباله از جمله دنبالههای عددی است که در طراحی سوالات مسابقات برنامهنویسی نیز استفاده میشود و گاهی در حل سوالات کاربرد دارد. از این رو آشنایی با روشهای مختلف تولید جملات آن حائز اهمیت است.
تعریف: دنبالهی اعداد فیبوناچی روی اعداد حسابی به صورت زیر تعریف میشود:
\[ F_n= \left \{\begin{matrix} F_{n-1} + F_{n-2} & & & \; n > 1\\ 1 & & & \; n = 1 \\ 0 & & & n = 0 \end{matrix}\right. \]
همانگونه که از تعریف مشخص است، جملات این دنباله از جمع دو جملهی قبلی آن با شروع از دو مقدار صفر و یک به دست میآید:
0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, ...
محاسبهی بازگشتی بر اساس تعریف
سادهترین راهکار برای محاسبهی اعداد دنبالهی فیبوناچی استفاده از تابع بازگشتی زیر است:
longlong fibo_1(int n){
if(n < 2)
return n;
return fibo_1(n - 1) + fibo_1(n - 2);
}
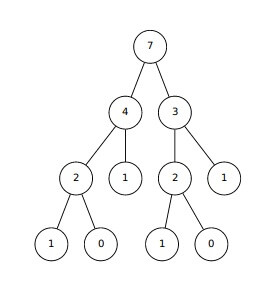
این تابع فراخوانی تابع با مقدار $n $ را به فراخوانی بازگشتی با دو مقدار بسیار نزدیک به $n$ تبدیل میکند. بنابراین میتوان پیشبینی کرد که زمان تولید خروجی نسبت به اندازهی ورودی از مرتبهی نمایی باشد. برای مثال فراخوانیهای بازگشتی تابع برای محاسبهی $F_7$ در شکل زیر آمده است:
به این ترتیب برای محاسبهی $F_7$ تابع مذکور $41$ بار فراخوانی میشود که در مقایسه با مقدار $n $ مقرون به صرفه نیست. دلیل این فراخوانیهای زیاد تکرار در محاسبهی جملات میانی است. به عنوان نمونه بر اساس شکل فوق مقدار $F_2$ هشت بار به صورت تکراری محاسبه شده است.
محاسبه با استفاده از روش برنامهنویسی پویا
برای رفع مشکل فراخوانیهای تکراری در محاسبات میتوان از روش برنامهنویسی پویا و حرکت از جزء به کل استفاده کرد:
longlong fibo_2(int n){
if(n < 2)
return n;
int f1 = 0, f2 = 1, f3;
for(int i = 2 ; i <= n ; i++){
f3 = f1 + f2;
f1 = f2;
f2 = f3;
}
return f3;
}
مرتبهی اجرایی محاسبهی جملهی $n$-ام دنبالهی فیبوناچی با این راهکار $ \Theta(n) $ است که در مقایسه با روش قبل (مرتبهی نمایی) عملکرد بسیار بهتری دارد. همچنین با توجه به کنار گذاشتن فراخوانیهای بازگشتی حافظهی کمتری مصرف میشود.
نکته: در صورتی که نیاز به در اختیار داشتن تمام جملات دنباله در یک بازهی مشخص باشد، این روش بهترین راهکار ممکن است و کافیست مقدار f3 در هر تکرار کد فوق در یک مخزن جدا مانند آرایه ذخیره شود.
محاسبه با استفاده از روش تقسیم و غلبه
تعریف رابطهی فیبوناچی خود به وضوح یک راهکار تقسیم و غلبه برای محاسبهی جملات آن است. اما همانگونه که بحث شد، استفاده از آن رابطه و فراخوانیهای بازگشتی مقرون به صرفه نیست.
یک تعریف بازگشتی دیگر دنبالهی فیبوناچی به صورت زیر است:
\[ \begin{matrix} F_{2n-1} = F^2_n + F^2_{n-1} \\ F_{2n} = (2 F_{n-1} + F_n) F_n \end{matrix} \]
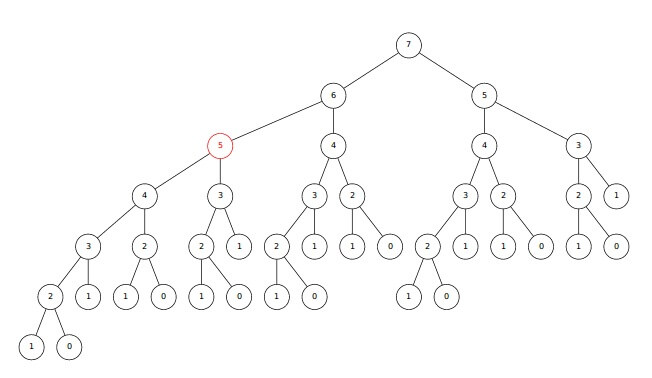
این رابطه محاسبهی مقدار جملهی $n$-ام دنباله را به محاسبهی دو جمله در حدود $ \frac{n}{2}$ تقسیم میکند. چنین رابطهای مرتبهی $ O(log\;n) $ را تداعی میکند. اما پیادهسازی بازگشتی این رابطه نیز فراخوانیهای تکراری دارد. به شکل زیر توجه کنید:
این راهکار تعداد فراخوانیها برای محاسبهی $F_7$ را از 41 فراخوانی حالت بازگشتی عادی به 11 فراخوانی کاهش میدهد. اما همچنان برخی فراخوانیهای تکراری وجود دارد که مرتبهی آن را بزرگتر از $ \Theta(n)$ (مرتبهی محاسبه به روش برنامهنویسی پویا) میکند. این فراخوانیهای تکراری زمانی که عدد جمله بزرگتر میشود، تاثیر چشمگیری در زمان محاسبه دارند.
برای رفع این مشکل و بالا بردن کارایی الگوریتم میتوان جملات تولید شده را در حافظه نگه داشت تا از محاسبهی مجدد آن جلوگیری کرد. در چنین حالتی اگرچه فضای مصرفی الگوریتم بالا میرود، اما زمان اجرای آن بهبود قابل توجهی پیدا میکند. به عنوان مثال برای محاسبهی جملهی $ F_{13941207} $ بیش از بیست میلیون فراخوانی تابع بدون ذخیره کردن مقادیر جملات کوچکتر صورت میگیرد (بسیار بیشتر از عدد $13941207$) که با ذخیره کردن این مقادیر به کمتر از $130$ فراخوانی کاهش مییابد!
نکته: ممکن است این سوال پیش بیاید که در روش فراخوانی بازگشتی با تعریف اصلی دنبالهی فیبوناچی نیز امکان ذخیره کردن جملات دنباله برای پیشگیری از محاسبهی مجدد آن وجود دارد. ویژگی مهم روش اخیر این است که تنها بخشی از اعداد دنباله تولید و ذخیره میشوند. در حالی که برای محاسبه با تعریف یا روش برنامهنویسی پویا باید تمامی جملات قبلی دنباله تولید و ذخیره شوند. به عنوان مثال، برای محاسبهی $F_{13941207}$ با راهکار اخیر تنها نیاز به ذخیره کردن $64 $ جمله است که در مقایسه با تمامی جملات بسیار کمتر است.
محاسبه با استفاده از روش ماتریسی
دنبالهی فیبوناچی را میتوان به فرم ماتریسی زیر نشان داد:
\[ \begin{pmatrix} F_n \\ F_{n-1} \end{pmatrix} = \begin{pmatrix} 1 & 1 \\ 1 & 0 \end{pmatrix} \begin{pmatrix} F_{n-1} \\ F_{n-2} \end{pmatrix} \]
با بسط دادن سمت راست رابطه، برابری زیر حاصل میشود:
\[ \begin{pmatrix} F_n \\ F_{n-1} \end{pmatrix} = M^{n-1} \begin{pmatrix} F_1 \\ F_0 \end{pmatrix} = M^{n-1} \begin{pmatrix} 1 \\ 0 \end{pmatrix}\; \; , \; \; M = \begin{pmatrix} 1 & 1 \\ 1 & 0 \end{pmatrix} \]
به عبارت دیگر، درایهی سطر اول حاصلضرب توان $(n-1)$-ام ماتریس $ M $ در ماتریس ستونی یک و صفر همان $ F_n $ است. بنابراین کافی است عنصر $ {(M^{n-1})}_{11} $ (عنصر سطر اول و ستون اول) محاسبه شود (چرا؟).
این رابطه محاسبهی جملات دنبالهی فیبوناچی را به محاسبهی توان یک ماتریس بدل میکند. توان یک عدد یا یک ماتریس مربعی را میتوان با استفاده از رابطهی زیر حساب کرد که همواره از مرتبهی $ O(log \; n)$ است (چرا؟):
\[ A^n= \left \{ \begin{matrix} {(A^{\frac{n}{2}})}^2 & & & \; n \% 2 = 0 \\ {(A^{\frac{n - 1}{2}})}^2 \times A & & & \; n \% 2 = 1 \end{matrix} \right. \]
مزیت بزرگ این روش نسبت به روش قبلی عدم نیاز به ذخیرهسازی مقادیر جملات کوچکتر است و در مقابل هزینهی سنگینتر محاسبهی ضرب اعداد را دارد که با توجه به کم بودن آنها (مرتبهی لگاریتمی) قابل چشمپوشی است. همینطور تعداد فراخوانیهای بازگشتی کمتری نسبت به روش قبلی دارد. به عنوان مثال، با این روش تنها $24$ فراخوانی بازگشتی برای محاسبهی توان $13941206$-ام ماتریس $ M $ و در نتیجه محاسبهی $F_{13941207} $ نیاز است.